Construct a PCovR Map

import numpy as np
from matplotlib import cm
from matplotlib import pyplot as plt
from sklearn.datasets import load_diabetes
from sklearn.kernel_ridge import KernelRidge
from sklearn.linear_model import Ridge
from sklearn.preprocessing import StandardScaler

from skmatter.decomposition import KernelPCovR, PCovR


cmapX = cm.plasma
cmapy = cm.Greys

For this, we will use the sklearn.datasets.load_diabetes() dataset from sklearn.

X, y = load_diabetes(return_X_y=True)
y = y.reshape(X.shape[0], -1)

X_scaler = StandardScaler()
X_scaled = X_scaler.fit_transform(X)

y_scaler = StandardScaler()
y_scaled = y_scaler.fit_transform(y)

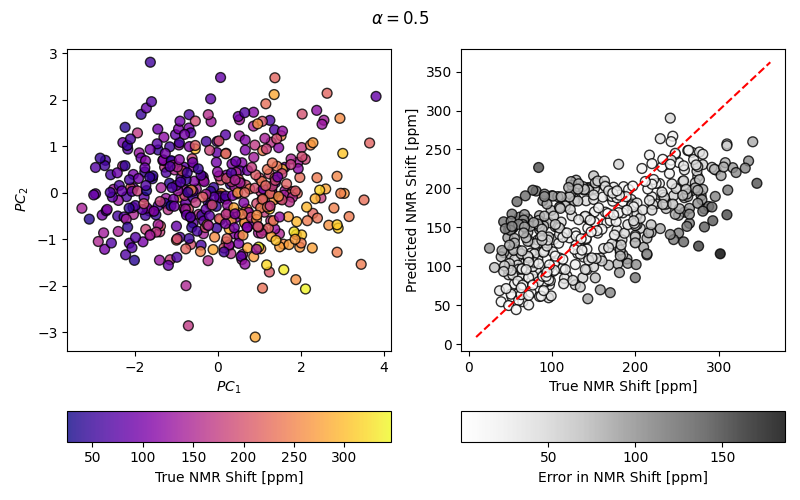
Computing a simple PCovR and making a fancy plot of the results

mixing = 0.5
pcovr = PCovR(
    mixing=mixing,
    regressor=Ridge(alpha=1e-8, fit_intercept=False, tol=1e-12),
    n_components=2,
)
pcovr.fit(X_scaled, y_scaled)
T = pcovr.transform(X_scaled)
yp = y_scaler.inverse_transform(pcovr.predict(X_scaled).reshape(-1, 1))

fig, ((axT, axy), (caxT, caxy)) = plt.subplots(
    2, 2, figsize=(8, 5), gridspec_kw=dict(height_ratios=(1, 0.1))
)

scatT = axT.scatter(T[:, 0], T[:, 1], s=50, alpha=0.8, c=y, cmap=cmapX, edgecolor="k")
axT.set_xlabel(r"$PC_1$")
axT.set_ylabel(r"$PC_2$")
fig.colorbar(scatT, cax=caxT, label="True NMR Shift [ppm]", orientation="horizontal")

scaty = axy.scatter(y, yp, s=50, alpha=0.8, c=np.abs(y - yp), cmap=cmapy, edgecolor="k")
axy.plot(axy.get_xlim(), axy.get_xlim(), "r--")
fig.suptitle(r"$\alpha=$" + str(mixing))

axy.set_xlabel(r"True NMR Shift [ppm]")
axy.set_ylabel(r"Predicted NMR Shift [ppm]")
fig.colorbar(
    scaty, cax=caxy, label="Error in NMR Shift [ppm]", orientation="horizontal"
)

fig.tight_layout()

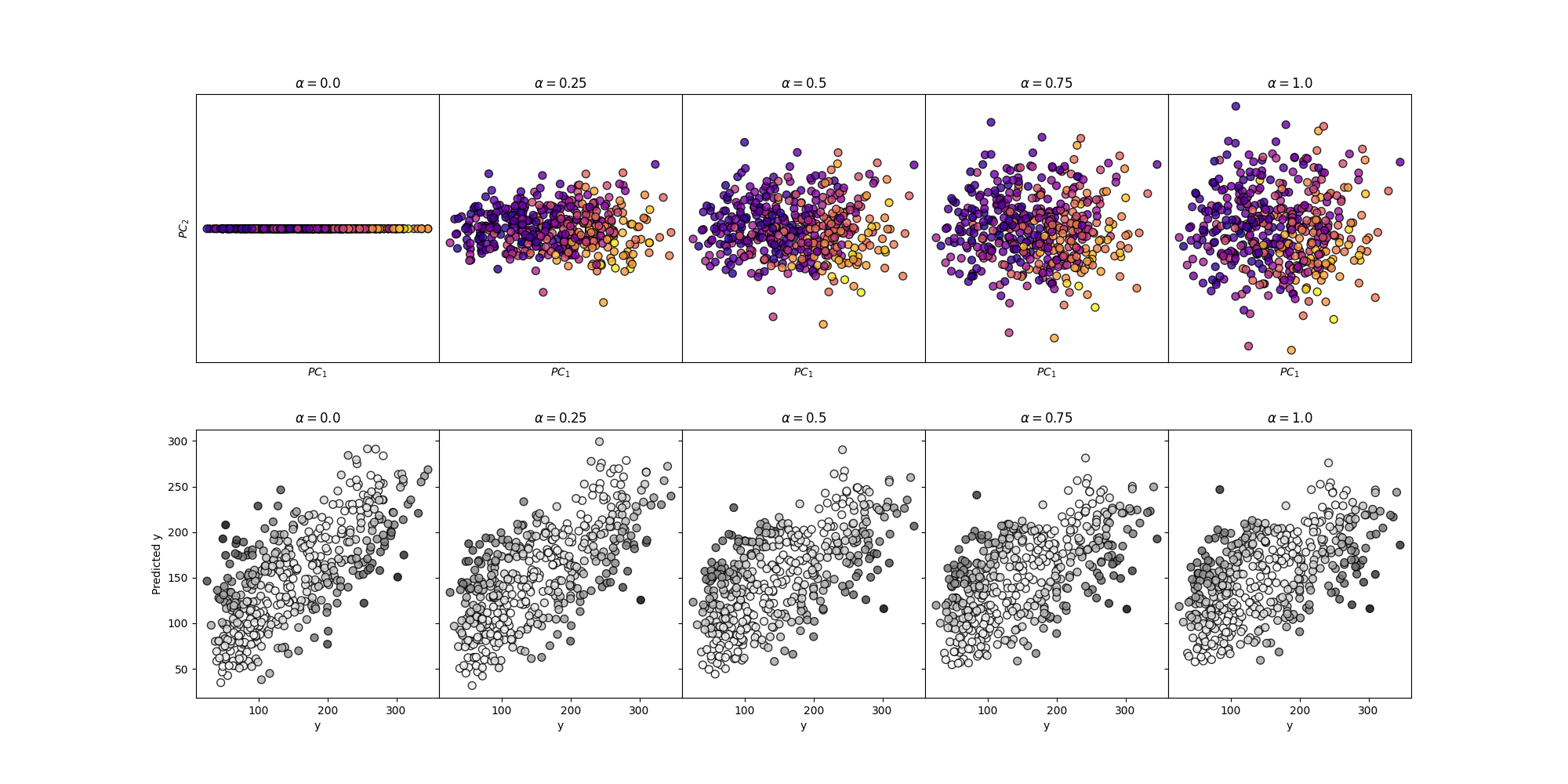
Surveying many Mixing Parameters

n_alpha = 5

fig, axes = plt.subplots(2, n_alpha, figsize=(4 * n_alpha, 10), sharey="row")

for i, mixing in enumerate(np.linspace(0, 1, n_alpha)):
    pcovr = PCovR(
        mixing=mixing,
        regressor=Ridge(alpha=1e-8, fit_intercept=False, tol=1e-12),
        n_components=2,
    )
    pcovr.fit(X_scaled, y_scaled)
    T = pcovr.transform(X_scaled)
    yp = y_scaler.inverse_transform(pcovr.predict(X_scaled).reshape(-1, 1))

    axes[0, i].scatter(
        T[:, 0], T[:, 1], s=50, alpha=0.8, c=y, cmap=cmapX, edgecolor="k"
    )
    axes[0, i].set_title(r"$\alpha=$" + str(mixing))
    axes[0, i].set_xlabel(r"$PC_1$")
    axes[0, i].set_xticks([])
    axes[0, i].set_yticks([])

    axes[1, i].scatter(
        y, yp, s=50, alpha=0.8, c=np.abs(y - yp), cmap=cmapy, edgecolor="k"
    )
    axes[1, i].set_title(r"$\alpha=$" + str(mixing))
    axes[1, i].set_xlabel("y")

axes[0, 0].set_ylabel(r"$PC_2$")
axes[1, 0].set_ylabel("Predicted y")

fig.subplots_adjust(wspace=0, hspace=0.25)
plt.show()

Construct a Kernel PCovR Map

Moving from PCovR to KernelPCovR is much like moving from PCA to KernelPCA in sklearn. Like KernelPCA, KernelPCovR can compute any pairwise kernel supported by sklearn or operate on a precomputed kernel.

mixing = 0.5
kpcovr = KernelPCovR(
    mixing=mixing,
    regressor=KernelRidge(
        alpha=1e-8,
        kernel="rbf",
        gamma=0.1,
    ),
    kernel="rbf",
    gamma=0.1,
    n_components=2,
)
kpcovr.fit(X_scaled, y_scaled)
T = kpcovr.transform(X_scaled)
yp = y_scaler.inverse_transform(kpcovr.predict(X_scaled).reshape(-1, 1))

fig, ((axT, axy), (caxT, caxy)) = plt.subplots(
    2, 2, figsize=(8, 5), gridspec_kw=dict(height_ratios=(1, 0.1))
)

scatT = axT.scatter(T[:, 0], T[:, 1], s=50, alpha=0.8, c=y, cmap=cmapX, edgecolor="k")
axT.set_xlabel(r"$PC_1$")
axT.set_ylabel(r"$PC_2$")
fig.colorbar(scatT, cax=caxT, label="y", orientation="horizontal")

scaty = axy.scatter(y, yp, s=50, alpha=0.8, c=np.abs(y - yp), cmap=cmapy, edgecolor="k")
axy.plot(axy.get_xlim(), axy.get_xlim(), "r--")
fig.suptitle(r"$\alpha=$" + str(mixing))

axy.set_xlabel(r"$y$")
axy.set_ylabel(r"Predicted $y$")
fig.colorbar(scaty, cax=caxy, label="Error in y", orientation="horizontal")

fig.tight_layout()

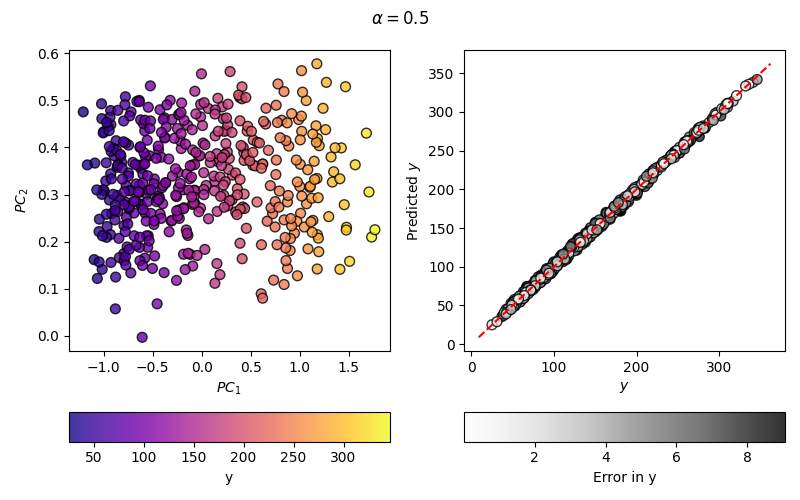
As you can see, the regression error has decreased considerably from the linear case, meaning that the map on the left can, and will, better correlate with the target values.

Note on KernelPCovR for Atoms, Molecules, and Structures

Applying this to datasets involving collections of atoms and their atomic descriptors, it’s important to consider the nature of the property you are learning and the samples you are comparing before constructing a kernel, for example, whether the analysis is to be based on whole structures or individual atomic environments. For more detail, see Appendix C of Helfrecht 2020 or, regarding kernels involving gradients, Musil 2021.