KPCovC Hyperparameter Tuning

import matplotlib as mpl
import matplotlib.pyplot as plt

from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import KernelPCA
from skmatter.decomposition import KernelPCovC

plt.rcParams["image.cmap"] = "tab20"
plt.rcParams["scatter.edgecolors"] = "k"

random_state = 0
n_components = 2

For this, we will use the sklearn.datasets.make_circles() dataset from sklearn.

X, y = datasets.make_circles(
    noise=0.1, factor=0.7, random_state=random_state, n_samples=1500
)

Original Data

fig, ax = plt.subplots(figsize=(5.5, 5))
ax.scatter(X[:, 0], X[:, 1], c=y)
ax.set_title("Original Data")

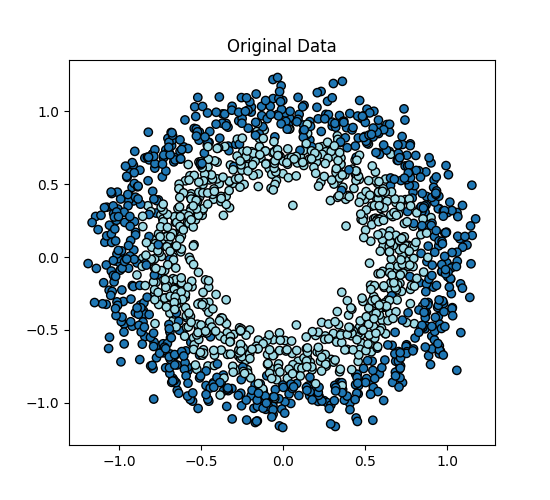
Text(0.5, 1.0, 'Original Data')

Scale Data

scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

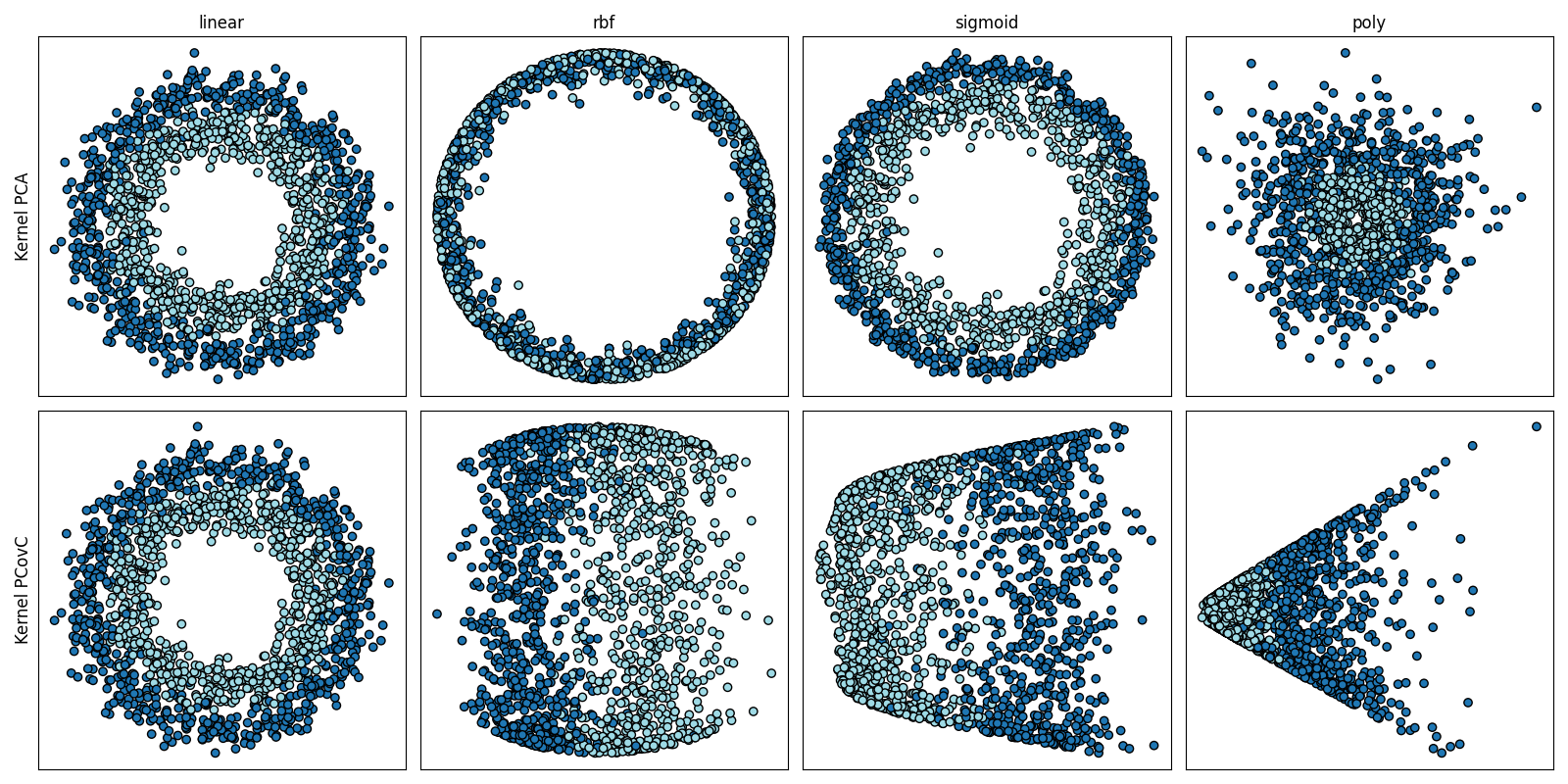
Effect of Kernel on KPCA and KPCovC Projections

Here, we see how Kernel PCovC with kernels such as a radial basis function can outperform Kernel PCA by producing cleanly separable projections from noisy circular data.

kernels = ["linear", "rbf", "sigmoid", "poly"]
kernel_params = {
    "rbf": {"gamma": 0.5},
    "sigmoid": {"gamma": 1.0},
    "poly": {"degree": 6},
}

fig, axs = plt.subplots(2, len(kernels), figsize=(len(kernels) * 4, 8))

center = True
mixing = 0.10

for i, kernel in enumerate(kernels):
    kpca = KernelPCA(
        random_state=random_state,
        n_components=n_components,
        kernel=kernel,
        **kernel_params.get(kernel, {}),
    )
    t_kpca = kpca.fit_transform(X_scaled)

    kpcovc = KernelPCovC(
        n_components=n_components,
        mixing=mixing,
        kernel=kernel,
        random_state=random_state,
        **kernel_params.get(kernel, {}),
        center=center,
    )
    t_kpcovc = kpcovc.fit_transform(X_scaled, y)

    axs[0][i].scatter(t_kpca[:, 0], t_kpca[:, 1], c=y)
    axs[1][i].scatter(t_kpcovc[:, 0], t_kpcovc[:, 1], c=y)

    axs[0][i].set_title(kernel)

    axs[0][i].set_xticks([])
    axs[1][i].set_xticks([])
    axs[0][i].set_yticks([])
    axs[1][i].set_yticks([])

axs[0][0].set_ylabel("Kernel PCA", fontsize=mpl.rcParams["axes.titlesize"])
axs[1][0].set_ylabel("Kernel PCovC", fontsize=mpl.rcParams["axes.titlesize"])

fig.subplots_adjust(wspace=0, hspace=0)
plt.tight_layout()

Decision Boundary Formation with Gamma Tuning

Depending on the data, tuning gamma values for the KPCovC kernel can greatly improve latent space projections, enabling clearer decision boundaries.

gamma_vals = [0.001, 0.0016, 0.00165, 0.00167, 0.00169, 0.00175]

fig, axs = plt.subplots(1, len(gamma_vals), figsize=(len(gamma_vals) * 3.5, 3.5))

for ax, gamma in zip(axs, gamma_vals):
    kpcovc = KernelPCovC(
        n_components=n_components,
        random_state=random_state,
        mixing=mixing,
        center=center,
        kernel="rbf",
        gamma=gamma,
    )
    t_kpcovc = kpcovc.fit_transform(X_scaled, y)

    ax.scatter(t_kpcovc[:, 0], t_kpcovc[:, 1], c=y)
    ax.set_title(f"gamma: {gamma}")

    ax.set_xticks([])
    ax.set_yticks([])

fig.subplots_adjust(wspace=0)
plt.tight_layout()